Last time, I wrote about how to speed up spell checking using a trie (also known as a prefix tree). However, for large dictionaries, a trie can waste a lot of memory. If you're trying to squeeze an application into a mobile device, every kilobyte counts. Consider this trie, with two words in it.

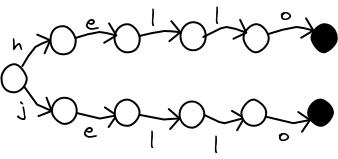
It can be shortened in a way so that any program accessing it would not even notice.

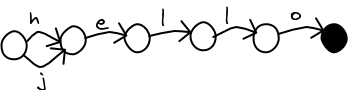
As early as 1988, Scrabble^TM programs were using structures like the above to shrink the their dictionaries. Over the years, the structure has been called many things. Some web pages call it a DAWG (Direct Acyclic Word Graph). But computer scientists have adopted the name "Minimal Acyclic Finite State Automaton", because some papers were already using the name DAWG for something else.

The most obvious way to build a MA-FSA, as suggested in many other web pages, is to first build the trie, and look for duplicate branches. I tried this on a list of 7 million words that I had. I wrote the algorithm in C++, but no matter how hard I tried, I kept running out of memory. A trie (or prefix tree) uses a lot of memory compared to a DAWG. It would be much better if one could create the DAWG right away, without first creating a trie. Jan Duciuk describes such a method in his paper. The central idea is to check for duplicates after you insert each word, so that the structure never gets huge.

1. Ensure that words are inserted in alphabetical order. That way, when you insert a word, you will then know for sure whether the previous word ended an entire branch. For example, "cat" followed by "catnip" does not result in a branch, because the s just added to the end. But when you follow it with "cats" you know that the "nip" part of the previous word needs checking.
2. Each time you complete a branch in the trie, check it for duplicate nodes. When a duplicate is found, redirect all incoming edges to the existing one and eliminate the duplicate.

The paper that I am paraphrasing, by Jan Daciuk and others, also describes a way to insert words out of order. But it is more complicated. In most cases, you can arrange to add your words in alphabetical order.

What's a duplicate node?

Two nodes are considered the same if they are both the final part of a word, or they are both not the final part of a word. They also need to have exactly the same edges pointing to exactly the same other nodes.

We start eliminating duplicates starting from the bottom of the branch, so each elimination can reveal more duplicates. Eventually, the branch of the trie zips together with a prior branch.

Step 1:

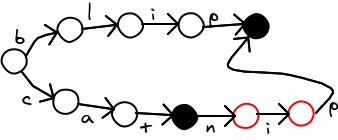
Several steps later:

Why go through so much trouble?

If you have a large word list, you could run it through gzip and get much better compression. The reason for storing a dictionary this way is to save space and remain easily searchable, without needing to decompress it first. Tries and MA-FSAs can support fuzzy search and prefix queries, so you can do spell checking and auto-completion. They can easily scale up to billions of entries. They have even been used to store large portions of the human genome. If you don't care about memory or speed, just store your words in an SQL database, or spin up 100 machines "in the cloud". I don't mind. More power to you!

MA-FSAs can be stored in as little as 4 bytes per edge-connector, as described by this web page.

Implementation

#!/usr/bin/python
# By Steve Hanov, 2011. Released to the public domain.
import sys
import time

DICTIONARY = "/usr/share/dict/words"
QUERY = sys.argv[1:]

# This class represents a node in the directed acyclic word graph (DAWG). It
# has a list of edges to other nodes. It has functions for testing whether it
# is equivalent to another node. Nodes are equivalent if they have identical
# edges, and each identical edge leads to identical states. The __hash__ and
# __eq__ functions allow it to be used as a key in a python dictionary.
class DawgNode:
    NextId = 0
    
    def __init__(self):
        self.id = DawgNode.NextId
        DawgNode.NextId += 1
        self.final = False
        self.edges = {}

    def __str__(self):        
        arr = []
        if self.final: 
            arr.append("1")
        else:
            arr.append("0")

        for (label, node) in self.edges.iteritems():
            arr.append( label )
            arr.append( str( node.id ) )

        return "_".join(arr)

    def __hash__(self):
        return self.__str__().__hash__()

    def __eq__(self, other):
        return self.__str__() == other.__str__()

class Dawg:
    def __init__(self):
        self.previousWord = ""
        self.root = DawgNode()

        # Here is a list of nodes that have not been checked for duplication.
        self.uncheckedNodes = []

        # Here is a list of unique nodes that have been checked for
        # duplication.
        self.minimizedNodes = {}

    def insert( self, word ):
        if word < self.previousWord:
            raise Exception("Error: Words must be inserted in alphabetical " +
                "order.")

        # find common prefix between word and previous word
        commonPrefix = 0
        for i in range( min( len( word ), len( self.previousWord ) ) ):
            if word[i] != self.previousWord[i]: break
            commonPrefix += 1

        # Check the uncheckedNodes for redundant nodes, proceeding from last
        # one down to the common prefix size. Then truncate the list at that
        # point.
        self._minimize( commonPrefix )

        # add the suffix, starting from the correct node mid-way through the
        # graph
        if len(self.uncheckedNodes) == 0:
            node = self.root
        else:
            node = self.uncheckedNodes[-1][2]

        for letter in word[commonPrefix:]:
            nextNode = DawgNode()
            node.edges[letter] = nextNode
            self.uncheckedNodes.append( (node, letter, nextNode) )
            node = nextNode

        node.final = True
        self.previousWord = word

    def finish( self ):
        # minimize all uncheckedNodes
        self._minimize( 0 );

    def _minimize( self, downTo ):
        # proceed from the leaf up to a certain point
        for i in range( len(self.uncheckedNodes) - 1, downTo - 1, -1 ):
            (parent, letter, child) = self.uncheckedNodes[i];
            if child in self.minimizedNodes:
                # replace the child with the previously encountered one
                parent.edges[letter] = self.minimizedNodes[child]
            else:
                # add the state to the minimized nodes.
                self.minimizedNodes[child] = child;
            self.uncheckedNodes.pop()

    def lookup( self, word ):
        node = self.root
        for letter in word:
            if letter not in node.edges: return False
            node = node.edges[letter]

        return node.final

    def nodeCount( self ):
        return len(self.minimizedNodes)

    def edgeCount( self ):
        count = 0
        for node in self.minimizedNodes:
            count += len(node.edges)
        return count

        
dawg = Dawg()
WordCount = 0
words = open(DICTIONARY, "rt").read().split()
words.sort()
start = time.time()    
for word in words:
    WordCount += 1
    dawg.insert(word)
    if ( WordCount % 100 ) == 0: print "%dr" % WordCount,
dawg.finish()
print "Dawg creation took %g s" % (time.time()-start)    

EdgeCount = dawg.edgeCount()
print "Read %d words into %d nodes and %d edges" % ( WordCount,
        dawg.nodeCount(), EdgeCount )
print "This could be stored in as little as %d bytes" % (EdgeCount * 4)    

for word in QUERY:
    if not dawg.lookup( word ):
        print "%s not in dictionary." % word
    else:
        print "%s is in the dictionary." % word

Updated code on github: using a DAWG as a map

Extensions

A MA-FSA is great for testing whether words are in a dictionary. But in the form I gave, it's not possible to retrieve values associated with the words. It is possible to include associated values in the automaton. Such structures are called "Minimal Acyclic Finite State Transducers". In fact, the algorithm I above can be easily modified to include a value. However, it causes the number of nodes to blow up, and you are much better off using a minimal perfect hash function in addition to your MA-FSA to store your data. I discuss this in part 3.