Succinct Data Structures: Cramming 80,000 words into a Javascript file.

March 20, 2011

Let's continue our short tour of data structures for storing words. Today, we will over-optimize John Resig's Word Game. Along the way, we shall learn about a little-known branch of computer science, called succinct data structures.

John wants to load a large dictionary of words into a web application, so his Javascript program can quickly check if a word is in the dictionary. He could transfer the words as long string, separated by spaces. This doesn't take much space once it is gzip-compressed by the web server. However, we also have to consider the amount of memory used in the browser itself. In a mobile application, memory is at a premium. If the user switches tabs, everything not being used is swapped out to flash memory. This results in long pauses when switching back.

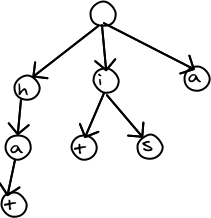
One of the best data structures for searching a dictionary is a trie. The speed of search does not depend on the number of words in the dictionary. It depends only on the number of letters in the word. For example, here is a trie containing the words "hat", "it", "is", and "a". The trie seems to compress the data, since words sharing the same beginnings only show up once.

We need to solve two problems. If we transmit the word list to the web browser, it then has to build the trie structure. This takes up a lot of time and memory. To save time, we could pre-encode the trie on the server in JSON format, which is parsed very quickly by the web browser. However, JSON is not a compact format, so some bandwidth is wasted downloading the data to the browser. We could avoid the wasted bandwidth by compressing the trie using a more compact format. The data is then smaller, but the web browser still has to decompress it to use it. In any case, the browser needs to create the trie in memory.

This leads us to the the second major problem. Despite appearances, tries use a lot of memory to store all of those links between nodes.

Fortunately, there is a way to store these links in a tiny amount of space.

Succinct Data Structures

Succinct data structures were introduced in Guy Jacobson's 1989 thesis, which you cannot read because it is not available anywhere. Fortunately, this important work has been referenced by many other papers since then.

A succinct data structure encodes data very efficiently, so that it does not need to be decoded to be used. Everything is accessed in-place, by reading bits at various positions in the data. To achieve optimal encoding, we use bits instead of bytes. All of our structures are encoded as a series of 0's and 1's.

Two important functions for succinct structures are:

rank(x) - returns the number of bits set to 1, up to and including position x
select(y) - returns the position of the yth 1. This is the inverse of the rank function. For example, if select(8) = 10, then rank(10) = 8.

Corresponding functions exist to find the rank/select of 0's instead of 1's. The rank function can be implemented in O(1) time using a lookup table (called a "directory"), which summarizes the number of 1's in certain parts of the string. The select() function is implemented in O(logn) time by performing binary search on the rank() function. It is possible to implement select in constant time, but it is complicated and space-hungry.

p	0	1	2	3	4	5	6	7
Bit	1	1	0	0	0	0	0	1
rank(p)	1	2	2	2	2	2	2	3
select(p)		0	1	7

A Succinct Trie

Here's a trie containing the words "hat", "is", "it", and "a".

First, we add a "super root". This is just an additional node above the root. It's there to make the math work out later.

We then process the nodes in level order -- that is, we go row by row and process the nodes left to right. We encode them to the bit string in that order.

In the picture below, I've labeled each node in level order for convenience. I've also placed the nodes encoding above it. The encoding is a "1" for each child, plus a 0. So a node with 5 children would be "111110" and a node with no children is "0".

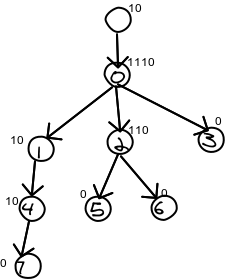
Now, we encode the nodes one after another. In the example, the bits would be 10111010110010000. I've separated them out in this table so you can see what's going on, but only the middle row is actually stored.

Position	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Bit	1	0	1	1	1	0	1	0	1	1	0	0	1	0	0	0	0
Node			0				1		2			3	4		5	6	7

We then encode the data for each node after that. To get the data for a given node, just read it directly from that node's index in the data array.

hiaatst

Getting the data

The main thing that we want to do with a trie is follow links from each node to its children. Using our encoding, we can follow a link using a simple formula. If a node is numbered i, then the number of its first child is select₀(i + 1) - i. The second child is the one after that, and so forth. To obtain the number of children, look up the first child of the i+1th node and subtract, since they are stored consecutively.

For example: We want the first child of node 2. The 3rd 0 is at position 7. Seven minus two is five. Therefore the first child is numbered 5. Similarly the first child of node 3 is found to be 7 by this formula (no, it doesn't really exist, but it works for the calculation). So node 2 has 7 minus 5 equals 2 children.

Demo

Here is a demonstration, hosted on my faster server. (Source code: Bits.js) (It doesn't work in RSS readers -- go to my blog to see it. Paste a list of words in the top text area (or click Load dictionary to load one). Click "Encode" to create the trie and encode it. This step can be very slow, because I did not optimize the encoding process. Once encoding is complete, you can use the Lookup button to check if words are in the dictionary.

Using this encoding method, a 611K dictionary containing 80000 words is compressed to 216K, or 132K gzipped. The browser does not need to decode it to use it. The whole trie takes as much space as a 216K string.

Your browser does not support iframes

Details

The directory contains the information needed to compute the rank and select functions quickly. The trie is the bitstring representing the trie and the connections between all of its nodes.

To avoid problems with UTF encoding formats and escaped characters, the bit strings are encoded in BASE-64. All of the bit decoding functions are configured to operated on BASE64 encoded units, so that the input string does not need to be decoded before being used.

We only handle the letters "a" to "z" in lower case. That way, we can encode each letter in 5 bits.

You can decrease space usage and performance by increasing the L2 constant, and setting L1 = L2*L2. This controls the number of bits summarized in each section of the rank directory. L2 is the maximum number of bits that have to be scanned to implement rank(). More bits means fewer directory entries, but the select() and rank() functions will take longer to scan the range of bits.

Caveats

I described how to create an MA-FSA in a previous article. There is no known way to succinctly encode one. You must store one pointer for each edge. However, as the number of words increases, an MA-FSA (also known as a DAWG) may eventually become more compact than the trie. This is because a trie does not compress common word endings together.