If you have a web site with a search function, you will rapidly realize that most mortals are terrible typists. Many searches contain mispelled words, and users will expect these searches to magically work. This magic is often done using levenshtein distance. In this article, I'll compare two ways of finding the closest matching word in a large dictionary. I'll describe how I use it on rhymebrain.com not for corrections, but to search 2.6 million words for rhymes, for every request, with no caching, on my super-powerful sock-drawer datacenter:

Algorithm #1

The levenshtein function take two words and returns how far apart they are. It's an O(N*M) algorithm, where N is the length of one word, and M is the length of the other. If you want to know how it works, go to this wikipedia page.

But comparing two words at a time isn't useful. Usually you want to find the closest matching words in a whole dictionary, possibly with many thousands of words. Here's a quick python program to do that, using the straightforward, but slow way. It uses the file /usr/share/dict/words. The first argument is the misspelled word, and the second argument is the maximum distance. It will print out all the words with that distance, as well as the time spent actually searching. For example:

smhanov@ubuntu1004:~$ ./method1.py goober 1
('goober', 0)
('goobers', 1)
('gooier', 1)
Search took 4.5575 s

Here's the program:

#!/usr/bin/python
#By Steve Hanov, 2011. Released to the public domain
import time
import sys

DICTIONARY = "/usr/share/dict/words";
TARGET = sys.argv[1]
MAX_COST = int(sys.argv[2])

# read dictionary file
words = open(DICTIONARY, "rt").read().split();

# for brevity, we omit transposing two characters. Only inserts,
# removals, and substitutions are considered here.
def levenshtein( word1, word2 ):
    columns = len(word1) + 1
    rows = len(word2) + 1

    # build first row
    currentRow = [0]
    for column in xrange( 1, columns ):
        currentRow.append( currentRow[column - 1] + 1 )

    for row in xrange( 1, rows ):
        previousRow = currentRow
        currentRow = [ previousRow[0] + 1 ]

        for column in xrange( 1, columns ):

            insertCost = currentRow[column - 1] + 1
            deleteCost = previousRow[column] + 1

            if word1[column - 1] != word2[row - 1]:
                replaceCost = previousRow[ column - 1 ] + 1
            else:                
                replaceCost = previousRow[ column - 1 ]

            currentRow.append( min( insertCost, deleteCost, replaceCost ) )

    return currentRow[-1]

def search( word, maxCost ):
    results = []
    for word in words:
        cost = levenshtein( TARGET, word )

        if cost <= maxCost:
            results.append( (word, cost) )

    return results

start = time.time()
results = search( TARGET, MAX_COST )
end = time.time()

for result in results: print result        

print "Search took %g s" % (end - start)

Runtime

For each word, we have to fill in an N x M table. An upper bound for the runtime is O( <number of words> * <max word length> ^2 )

Improving it

Sorry, now you need to know how the algorithm works and I'm not going to explain it. (You really need to read the wikipedia page.) The important things to know are that it fills in a N x M sized table, like this one, and the answer is in the bottom-right square.

		k	a	t	e
	0	1	2	3	4
c	1	1	2	3	4
a	2	2	1	2	3
t	3	3	2	1	2

But wait, what's it going to do when it moves on to the next word after cat? In my dictionary, that's "cats" so here it is:

		k	a	t	e
	0	1	2	3	4
c	1	1	2	3	4
a	2	2	1	2	3
t	3	3	2	1	2
s	4	4	3	2	2

Only the last row changes. We can avoid a lot of work if we can process the words in order, so we never need to repeat a row for the same prefix of letters. The trie data structure is perfect for this. A trie is a giant tree, where each node represents a partial or complete word. Here's one with the words cat, cats, catacomb, and catacombs in it (courtesy of zwibbler.com). Nodes that represent a word are marked in black.

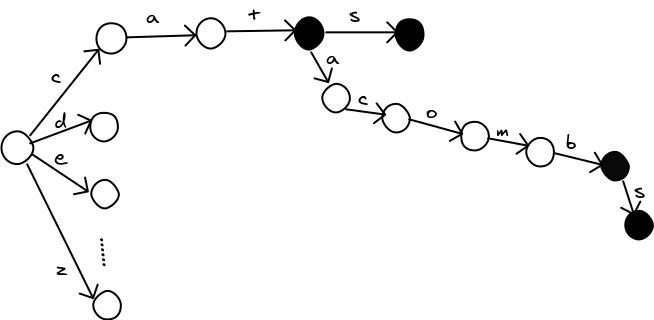
With a trie, all shared prefixes in the dictionary are collaped into a single path, so we can process them in the best order for building up our levenshtein tables one row at a time. Here's a python program to do that:

#!/usr/bin/python
#By Steve Hanov, 2011. Released to the public domain
import time
import sys

DICTIONARY = "/usr/share/dict/words";
TARGET = sys.argv[1]
MAX_COST = int(sys.argv[2])

# Keep some interesting statistics
NodeCount = 0
WordCount = 0

# The Trie data structure keeps a set of words, organized with one node for
# each letter. Each node has a branch for each letter that may follow it in the
# set of words.
class TrieNode:
    def __init__(self):
        self.word = None
        self.children = {}

        global NodeCount
        NodeCount += 1

    def insert( self, word ):
        node = self
        for letter in word:
            if letter not in node.children: 
                node.children[letter] = TrieNode()

            node = node.children[letter]

        node.word = word

# read dictionary file into a trie
trie = TrieNode()
for word in open(DICTIONARY, "rt").read().split():
    WordCount += 1
    trie.insert( word )

print "Read %d words into %d nodes" % (WordCount, NodeCount)

# The search function returns a list of all words that are less than the given
# maximum distance from the target word
def search( word, maxCost ):

    # build first row
    currentRow = range( len(word) + 1 )

    results = []

    # recursively search each branch of the trie
    for letter in trie.children:
        searchRecursive( trie.children[letter], letter, word, currentRow, 
            results, maxCost )

    return results

# This recursive helper is used by the search function above. It assumes that
# the previousRow has been filled in already.
def searchRecursive( node, letter, word, previousRow, results, maxCost ):

    columns = len( word ) + 1
    currentRow = [ previousRow[0] + 1 ]

    # Build one row for the letter, with a column for each letter in the target
    # word, plus one for the empty string at column 0
    for column in xrange( 1, columns ):

        insertCost = currentRow[column - 1] + 1
        deleteCost = previousRow[column] + 1

        if word[column - 1] != letter:
            replaceCost = previousRow[ column - 1 ] + 1
        else:                
            replaceCost = previousRow[ column - 1 ]

        currentRow.append( min( insertCost, deleteCost, replaceCost ) )

    # if the last entry in the row indicates the optimal cost is less than the
    # maximum cost, and there is a word in this trie node, then add it.
    if currentRow[-1] <= maxCost and node.word != None:
        results.append( (node.word, currentRow[-1] ) )

    # if any entries in the row are less than the maximum cost, then 
    # recursively search each branch of the trie
    if min( currentRow ) <= maxCost:
        for letter in node.children:
            searchRecursive( node.children[letter], letter, word, currentRow, 
                results, maxCost )

start = time.time()
results = search( TARGET, MAX_COST )
end = time.time()

for result in results: print result        

print "Search took %g s" % (end - start)

Here are the results:

smhanov@ubuntu1004:~$ ./method1.py goober 1
Read 98568 words into 225893 nodes
('goober', 0)
('goobers', 1)
('gooier', 1)
Search took 0.0141618 s

The second algorithm is over 300 times faster than the first. Why? Well, we create at most one row of the table for each node in the trie. The upper bound for the runtime is O(<max word length> * <number of nodes in the trie>). For most dictionaries, considerably less than O(<number of words> * <max word length>^2)

Saving memory

Building a trie can take a lot of memory. In Part 2, I discuss how to construct a MA-FSA (or DAWG) which contains the same information in a more compact form.

RhymeBrain

In December, I realized that Google had released their N-grams data, a list of all of the words in all of the books that they have scanned for their Books search feature. When I imported them all into RhymeBrain, my dictionary size at once increased from 260,000 to 2.6 million, and I was having performance problems.

I already stored the words in a trie, indexed by pronunciation instead of letters. However, to search it, I was first performing a quick and dirty scan to find words that might possibly rhyme. Then I took that large list and ran each one through the levenshtein function to calculate RhymeRank^TM. The user is presented with only the top 50 entries of that list.

After a lot of deep thinking, I realized that the levenshtein function could be evaluated incrementally, as I described above. Of course, I might have realized this sooner if I had read one of the many scholarly papers on the subject, which describe this exact method. But who has time for that? :)

With the new algorithm, queries take between 19 and 50 ms even for really long words, but the best part is that I don't need to maintain two separate checks (quick and full), and the RhymeRank^TM algorithm is performed uniformly for each of the 2.6 million words on my 1GHz Acer Aspire One datacenter.

(Previous articles on RhymeBrain)

Other references

In his article How to write a spelling corrector, Peter Norvig approaches the problem using a different way of thinking. He first stores his dictionary in a hash-table for fast lookup. Then he goes through hundreds, or even thousands of combinations of spelling mutations of the target word and checks if each one is in the dictionary. This system is clever, but breaks down quickly if you want to find words with an error greater than 1. Also, it would not work for me, since I needed to modify the cost functions for insert, delete, and substitution.

In the blog article Fuzzy String Matching, the author presents a recursive solution using memoization (caching). This is equivalent to flood-filling a diagonal band across the table. It gives a runtime of O(k * <number of nodes in the trie>), where k is the maximum cost. You can modify my algorithm above to only fill in only some entries of the table. I tried it, but it made the examples too complex and actually slowed it down. I blame my python skills.

Update: I just realized the author has created a new solution for dictionary search, also based on tries. I quickly tried it on my machine and dictionary, and got a time of 0.009301, assuming the prefix tree is prebuilt. It's slightly faster for an edit distance of 1! But somethings going on, because it takes 1.5 s for an edit distance of 4, whereas my code takes only 0.44. Phew!

And of course, you could create a levenshtein automaton, essentially a big honking regular expression that matches all possible mispellings. But to do it efficiently you need to write big honking gobs of code. (The code in the linked article does not do it efficiently, but states that it is possible to do so.) Alternatively, you could enumerate all possible mispellings and insert them into a MA-FSA or DAWG to obtain the regular expression.

• Using a netbook as a webserver
• C++: A language for next-generation web apps