Throw away the keys: Easy, Minimal Perfect Hashing
This technique is described in Kowaltowski, T.; CL. Lucchesi (1993), "Applications of finite automata representing large vocabularies", Software-Practice and Experience 1993
Here's my implementation using an MA-FSA as a map: Github
In part 1 of this series, I described how to find the closest match in a dictionary of words using a Trie. Such searches are useful because users often mistype queries. But tries can take a lot of memory -- so much that they may not even fit in the 2 to 4 GB limit imposed by 32-bit operating systems.
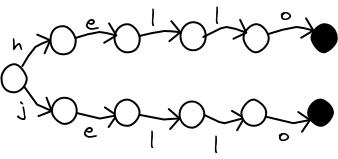
In part 2, I described how to build a MA-FSA (also known as a DAWG). The MA-FSA greatly reduces the number of nodes needed to store the same information as a trie. They are quick to build, and you can safely substitute an MA-FSA for a trie in the fuzzy search algorithm.
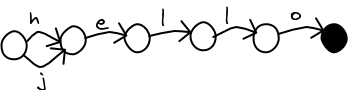
There is a problem. Since the last node in a word is shared with other words, it is not possible to store data in it. We can use the MA-FSA to check if a word (or a close match) is in the dictionary, but we cannot look up any other information about the word!
If we need extra information about the words, we can use an additional data structure along with the MA-FSA. We can store it in a hash table. Here's an example of a hash table that uses separate chaining. To look up a word, we run it through a hash function, H() which returns a number. We then look at all the items in that "bucket" to find the data. Since there should be only a small number of words in each bucket, the search is very fast.

Notice that the table needs to store the keys (the words that we want to look up) as well as the data associated with them. It needs them to resolve collisions -- when two words hash to the same bucket. Sometimes these keys take up too much storage space. For example, you might be storing information about all of the URLs on the entire Internet, or parts of the human genome. In our case, we already store the words in the MA-FSA, and it is redundant to duplicate them in the hash table as well. If we could guarantee that there were no collisions, we could throw away the keys of the hash table.
Minimal perfect hashing
Perfect hashing is a technique for building a hash table with no collisions. It is only possible to build one when we know all of the keys in advance. Minimal perfect hashing implies that the resulting table contains one entry for each key, and no empty slots.
We use two levels of hash functions. The first one, H(key), gets a position in an intermediate array, G. The second function, F(d, key), uses the extra information from G to find the unique position for the key. The scheme will always returns a value, so it works as long as we know for sure that what we are searching for is in the table. Otherwise, it will return bad information. Fortunately, our MA-FSA can tell us whether a value is in the table. If we did not have this information, then we could also store the keys with the values in the value table.
In the example below, the words "blue" and "cat" both hash to the same position using the H() function. However, the second level hash, F, combined with the d-value, puts them into different slots.

In step 1, we place the keys into buckets according to the first hash function, H.
In step 2, we process the buckets largest first and try to place all the keys it contains in an empty slot of the value table using F(d=1, key). If that is unsuccessful, we keep trying with successively larger values of d. It sounds like it would take a long time, but in reality it doesn't. Since we try to find the d value for the buckets with the most items early, they are likely to find empty spots. When we get to buckets with just one item, we can simply place them into the next unoccopied spot.
Here's some python code to demonstrate the technique. In it, we use H = F(0, key) to simplify things.
#!/usr/bin/python
# Easy Perfect Minimal Hashing
# By Steve Hanov. Released to the public domain.
#
# Based on:
# Edward A. Fox, Lenwood S. Heath, Qi Fan Chen and Amjad M. Daoud,
# "Practical minimal perfect hash functions for large databases", CACM, 35(1):105-121
# also a good reference:
# Compress, Hash, and Displace algorithm by Djamal Belazzougui,
# Fabiano C. Botelho, and Martin Dietzfelbinger
import sys
DICTIONARY = "/usr/share/dict/words"
TEST_WORDS = sys.argv[1:]
if len(TEST_WORDS) == 0:
TEST_WORDS = ['hello', 'goodbye', 'dog', 'cat']
# Calculates a distinct hash function for a given string. Each value of the
# integer d results in a different hash value.
def hash( d, str ):
if d == 0: d = 0x01000193
# Use the FNV algorithm from http://isthe.com/chongo/tech/comp/fnv/
for c in str:
d = ( (d * 0x01000193) ^ ord(c) ) & 0xffffffff;
return d
# Computes a minimal perfect hash table using the given python dictionary. It
# returns a tuple (G, V). G and V are both arrays. G contains the intermediate
# table of values needed to compute the index of the value in V. V contains the
# values of the dictionary.
def CreateMinimalPerfectHash( dict ):
size = len(dict)
# Step 1: Place all of the keys into buckets
buckets = [ [] for i in range(size) ]
G = [0] * size
values = [None] * size
for key in dict.keys():
buckets[hash(0, key) % size].append( key )
# Step 2: Sort the buckets and process the ones with the most items first.
buckets.sort( key=len, reverse=True )
for b in xrange( size ):
bucket = buckets[b]
if len(bucket) <= 1: break
d = 1
item = 0
slots = []
# Repeatedly try different values of d until we find a hash function
# that places all items in the bucket into free slots
while item < len(bucket):
slot = hash( d, bucket[item] ) % size
if values[slot] != None or slot in slots:
d += 1
item = 0
slots = []
else:
slots.append( slot )
item += 1
G[hash(0, bucket[0]) % size] = d
for i in range(len(bucket)):
values[slots[i]] = dict[bucket[i]]
if ( b % 1000 ) == 0:
print "bucket %d r" % (b),
sys.stdout.flush()
# Only buckets with 1 item remain. Process them more quickly by directly
# placing them into a free slot. Use a negative value of d to indicate
# this.
freelist = []
for i in xrange(size):
if values[i] == None: freelist.append( i )
for b in xrange( b, size ):
bucket = buckets[b]
if len(bucket) == 0: break
slot = freelist.pop()
# We subtract one to ensure it's negative even if the zeroeth slot was
# used.
G[hash(0, bucket[0]) % size] = -slot-1
values[slot] = dict[bucket[0]]
if ( b % 1000 ) == 0:
print "bucket %d r" % (b),
sys.stdout.flush()
return (G, values)
# Look up a value in the hash table, defined by G and V.
def PerfectHashLookup( G, V, key ):
d = G[hash(0,key) % len(G)]
if d < 0: return V[-d-1]
return V[hash(d, key) % len(V)]
print "Reading words"
dict = {}
line = 1
for key in open(DICTIONARY, "rt").readlines():
dict[key.strip()] = line
line += 1
print "Creating perfect hash"
(G, V) = CreateMinimalPerfectHash( dict )
for word in TEST_WORDS:
line = PerfectHashLookup( G, V, word )
print "Word %s occurs on line %d" % (word, line)
Experimental Results
I prepared separate lists of randomly selected words to test whether the runtime is really linear as claimed.| Number of items | Time (s) |
|---|---|
| 100000 | 2.24 |
| 200000 | 4.48 |
| 300000 | 6.68 |
| 400000 | 9.27 |
| 500000 | 11.71 |
| 600000 | 13.81 |
| 700000 | 16.72 |
| 800000 | 18.78 |
| 900000 | 21.12 |
| 1000000 | 24.816 |
Here's a pretty chart.

Comments