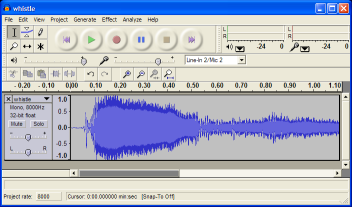
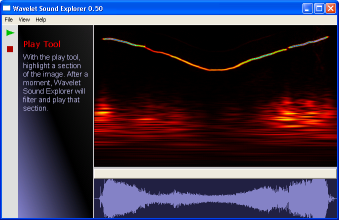
Listen to the sound file
Download Wavelet Sound Explorer 0.50 Updated February 9, 2008
Wavelet Sound Explorer is a freeware program for Windows that lets you view sound files in the frequency/time domain. It should be of interest to students in the areas of acoustics, phonetics, and anyone interested in sound.
Audio editing software such as Audacity, is still using ideas based on the record player. This is astounding given we have learned so much more about sound in the past 100 years.
In the record player, a needle carves grooves in the surface of the record. If you look at the grooves under a microscope, you would see a waveform -- the strength of the vibrations of the air needed to produce the recorded sound. Audio software such as Audacity presents this same information graphically.
The waveform is in the time domain -- that is, you can only see how the signal changes with time and amplitude. However, it is much more descriptive to present an audio signal in 3D -- which takes into account time, frequency, and amplitude. Compare the same file in Audacity and Wavelet Sound Explorer. Which one is more useful?


The aim of this project is to create an audio editor based on the continuous wavelet transform. The CWT is particularly convenient, since the original waveform can be reproduced simply by adding up the columns of the image.
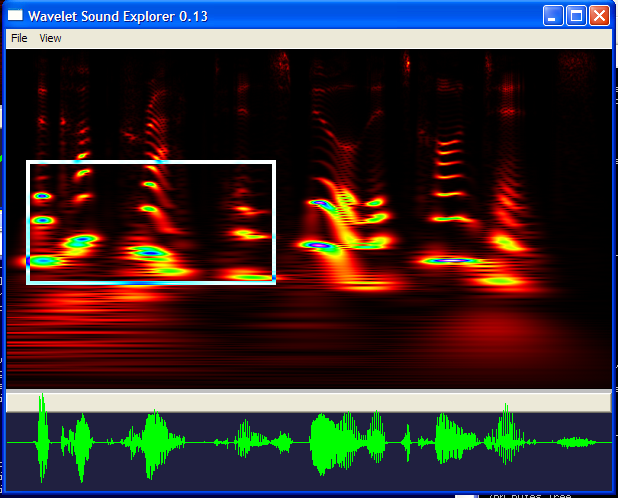
Here's an example of the program in action. Here is the wavelet transform of the sentence, "The cup cracked and spilled its contents". Notice the various bands in the image -- these are the formants that make up the human voice.
The power of this technique is evident when you select a region of the image -- it filters it and plays back only the portion that you select.
Listen to the selected region: cup-sel.wav
Because we calculate the full wavelet transform, and not just an approximation, we can zoom in to any level of detail. Here's the real part of a sound file. You can actually see the peaks of each wave.
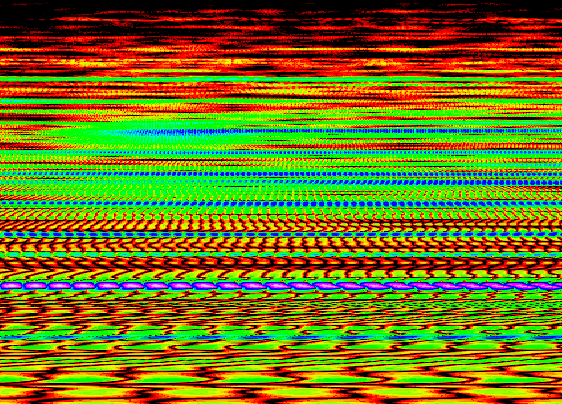
Modern operating systems have blazing fast disk access, so it's feasible to process these in a multi-gigabyte file. Or, if you are just interested in viewing the result and not reconstructing the original sound file, you can scale the image to whatever size you want. Right now, Wavelet Sound Explorer only has the capability to create the whole image and store it in memory, so it's only feasible to process short sound files of less than 10 seconds.
I've been focusing on getting the disk stuff working. If the wavelet transform won't fit into memory, it creates a file (usually several gigabytes) to work on. Because the fourier transform is slower than the writing to disk, and they are done at the same time, the disk part causes no overhead.
It is obscene how long the inverse FFT step takes. I'd like to do it using the method described in the oblique projections paper, but I haven't had a chance to figure out the math. Apparently, this method is O(N), whereas the FFT method is O(Nlog(N)). If it were that fast, we wouldn't have to store it on disk at all. It could just be recomputed on the fly whenever we need to display it.
| Math Trek | How old recordings can be restored in the frequency domain. |
| Spectrogram | This tool for Windows calculates the frequency/time chart in real time. It's based on the Short Time Fourier Transform, and it doesn't allow any editing. |
| The Wavelet Tutorial (By Robi Polikar) | This is simply the best tutorial available for wavelet theory. |
| Wavelet Whale Sounds | Mark Fischer records whale sounds, and creates stunning high resolution images as an art form. |
Wavelet Sound Explorer Source Code
Here is an algorithm in C++ to perform the continuous wavelet transform, in this case specifically the Morlet transform. I use the fftw library to perform the inverse Fourier transform. The source code is extracted from Wavelet Sound Explorer, and depends on many different parts of the program (for example, showing the percentage complete on the screen, and creating a windows bitmap of the results). However, it should be enough to get you started if you are interested in this stuff.
I developed this algorithm myself, based mostly on information in numerous papers and The Illustrated Wavelet Transform Handbook.
static int round_2_up(int num)
{
return (int)pow( 2, ceil(log((double)num)/log((double)2)) );
}
static float FTWavelet( float x, float scale, float f0 )
{
if ( x < 0.9 / scale || x > 1.1 / scale ) {
return (float)0.0;
}
static const float pi = (float)3.14159265358979323846;
static const double two_pi_f0 = 2.0 * pi * f0;
static const double multiplier = 1.8827925275534296252520792527491;
scale *= (float)f0;
// 1.88279*exp(-0.5*(2*pi*x*10-2*pi*10)^2)
float basic = (float)(multiplier *
exp(-0.5*(2*pi*x*scale-two_pi_f0)*(2*pi*x*scale-two_pi_f0)));
// pi^0.25*sqrt(2.0)*exp(-0.5*(2*pi*x*scale-2*pi*0.849)^2)
return sqrt(scale)*basic;
}
ScalogramCreator::ScalogramCreator( TaskObserver* observer ) :
Task<ScalogramCreatorParams>::Task( observer )
{
}
ScalogramCreator::~ScalogramCreator()
{
}
void
ScalogramCreator::run( ScalogramCreatorParams params )
{
unsigned avoid_overlap = (unsigned)(params.lowfreq * 20);
double df = pow(params.lowfreq/params.highfreq, 1.0 / (params.lowfreq-params.highfreq));
unsigned N = round_2_up( params.wave->size + avoid_overlap )*2;
params.image->upperScale = (float)params.lowfreq;
params.image->lowerScale = (float)params.highfreq;
params.image->sampleRate = params.wave->sampleRate;
fftwf_plan plan_forward;
fftwf_plan plan_inverse;
fftwf_complex* data = (fftwf_complex*) fftwf_malloc(sizeof(fftwf_complex) * N);
fftwf_complex* ans = (fftwf_complex*) fftwf_malloc(sizeof(fftwf_complex) * N);
plan_inverse = fftwf_plan_dft_1d(N, ans, ans, FFTW_BACKWARD, FFTW_ESTIMATE);
plan_forward = fftwf_plan_dft_1d(N, data, data, FFTW_FORWARD, FFTW_ESTIMATE );
memset( data, 0, sizeof(fftwf_complex)*N);
memset( ans, 0, sizeof(fftwf_complex)*N);
printf("\n");
for( unsigned i =0 ; i < params.wave->size; i++ ) {
data[i][0] = (float)params.wave->samples[i];
}
fftwf_execute(plan_forward);
// for each scale level,
int row = 0;
int ticks = GetTickCount();
for ( double period = params.highfreq; period <= params.lowfreq; period *= df, row += 1 )
{
printf("%d: %g \r", row, period);
if ( GetTickCount() -ticks > 500 ) {
setProgress( (double)row / params.image->bands );
ticks = GetTickCount();
}
if ( _stopRequested ) {
break;
}
for( int i = 0; i < (int)N/2; i++ ) {
ans[i][0] = FTWavelet( (float)i, (float)period/(N), (float)params.f0 ) * data[i][0];
ans[i][1] = 0;
ans[N-i-1][0] = 0;
ans[N-i-1][1] = 0;
}
fftwf_execute(plan_inverse);
params.image->addRow( row, (float*)ans );
params.image->renderRowToDib( row, params.dib, params.type, params.map, 0,
params.wave->size, (float*)ans );
}
fftwf_destroy_plan(plan_forward);
fftwf_destroy_plan(plan_inverse);
fftwf_free(data);
fftwf_free(ans);
if ( !_stopRequested ) {
for ( int i = 0; i < (int)params.image->bands; i++ ) {
params.image->renderRowToDib( i, params.dib, params.type, params.map, 0,
params.wave->size );
}
}
}