Let's say you have millions of pictures of faces tagged with names. Given a new photo, how do you find the name of person that the photo most resembles?

Suppose you have scanned short sections of millions of songs, and for each five second period you have a rough list of the frequencies and beat patterns contained in them. Given a new audio snippet, can you find the song to which it belongs?

What if you have data from thousands of web site users, including usage frequency, when they signed up, what actions they took, etc. Given a new user's actions, can you find other users like them and predict whether they will upgrade or stop using your product?

In the cases I mentioned, each record has hundreds or thousands of elements: the pixels in a photo, or patterns in a sound snippet, or web usage data. These records can be regarded as points in high dimensional space. When you look at a points in space, they tend to form clusters, and you can infer a lot by looking at ones nearby.

In this blog entry, I will half-heartedly describe some data structures for spatial search. Then I will launch into a detailed explanation of VP-Trees (Vantage Point Trees), which are simple, fast, and can easily handle low or high dimensional data.

Data structures for spatial search

When a programmer wants to search for points in space, perhaps the the first data structure that springs to mind is the K-D tree. In this structure, we repeatedly subdivide all of the points along a particular dimension to form a tree structure.

With high dimensional data, the benefits of the K-D tree are soon lost. As the number of dimensions increase, the points tend to scatter and it becomes difficult to pick a good splitting dimension. Hundreds of students have gotten their masters degree by coding up K-D trees and comparing them with an alphabet soup of other trees. (In particular, I like this one.)

The authors of Data Mining: Practical machine Learning Tools and Techniques suggests using Ball Trees. Each node of a Ball tree describes a bounding sphere, using a centre and a radius. To make the search efficient, the nodes should use the minimal sphere that completely contains all of its children, and overlaps the least with other sibling spheres in the tree.

Ball trees work, but they are difficult to construct. It is hard to figure out the optimal placement of spheres to minimize the overlap. For high dimensional data, the structure can be huge. The nodes must store their centre, and if a point has thousands of coordinates, it occupies a lot of storage. Moreover, you need to be able to calculate these fake sphere centres from the other points. What, exactly, does it mean to calculate a point between two sets of users' web usage history?

Fortunately, there are methods of building tree structures which do not require manipulation of the individual coordinates. The things that you put in them do not need to resemble points. You only need a way to figure out how far apart they are.

Entering metric space

Image you are blindfolded and placed in a gymnasium filled with other blindfolded people. Even worse: you also lost all sense of direction. When others talk, you can sense how far away they are, but not where they are in the room. Eventually, some basic laws become clear.

1. If there is no distance between you and the other person, you are standing in the same spot.
2. When you talk to another person, they perceive you has being the same distance away as you perceive them.
3. When you talk to person A and person B, the distance to A is always less than the distance to B plus the distance from A to B. In other words, the shortest distance between two people is a straight line. Distance is never negative.

This is a metric space. The great thing about metric spaces is that the things that you put in them do not need to do a lot. All you need is a way of calculating the distances between them. You do not need to be able to add them together or find bounding shapes or find points midway between them. The data structure that I want to talk about is the Vantage Point Tree (a generalization of the BK-tree that is eloquently reviewed in Damn cool algorithms.

Each node of the tree contains one of the input points, and a radius. Under the left child are all points which are closer to the node's point than the radius. The other child contains all of the points which are farther away. The tree requires no other knowledge about the items in it. All you need is a distance function that satisfies the properties of a metric space.

How searching a VP-Tree works

Let us examine one of these nodes in detail, and what happens during a recursive search for the nearest neighbours to a target.

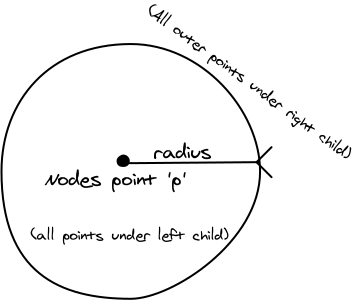
Suppose we want to find the two nearest neighbours to the target, marked with the red X. Since we have no points yet, the node's center p is the closest candidate, and we add it to the list of results. (It might be bumped out later). At the same time, we update our variable tau which tracks the distance of the farthest point that we have in our results.

Then, we have to decide whether to search the left or right child first. We may end up having to search them both, but we would like to avoid that most of the time.

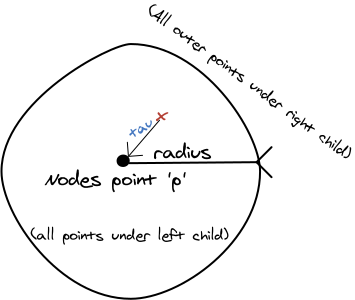
Since the target is closer to the node's center than its outer shell, we search the left child first, which contains all of the points closer than the radius. We find the blue point. Since it is farther away than tau we update the tau value.

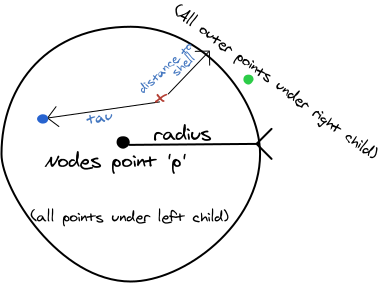
Do we need to continue the search? We know that we have considered all the points that are within the distance radius of p. However, it is closer to get to the outer shell than the farthest point that we have found. Therefore there could be closer points just outside of the shell. We do need to descend into the right child to find the green point.

If, however, we had reached our goal of collecting the n nearest points, and the target point is farther from the the outer shell than the farthest point that we have collected, then we could have stopped looking. This results in significant savings.

Implementation

Here is an implementation of the VP Tree in C++. The recursive search() function decides whether to follow the left, right, or both children. To efficiently maintain the list of results, we use a priority queue. (See my article, Finding the top k items in a list efficiently for why).

I tried it out on a database of all the cities in the world, and the VP tree search was 3978 times faster than a linear search through all the points. You can download the C++ program that uses the VP tree for this purpose here.

It is worth repeating that you must use a distance metric that satisfies the triangle inequality. I spent a lot of time wondering why my VP tree was not working. It turns out that I had not bothered to find the square root in the distance calculation. This step is important to satisfy the requirements of a metric space, because if the straight line distance to a <= b+c, it does not necessarily follow that a² <= b² + c².

Here is the output of the program when you search for cities by latitude and longitude.

Create took 15484122
Search took 36
ca,waterloo,Waterloo,08,43.4666667,-80.5333333
 0.0141501
ca,kitchener,Kitchener,08,43.45,-80.5
 0.025264
ca,bridgeport,Bridgeport,08,43.4833333,-80.4833333
 0.0396333
ca,elmira,Elmira,08,43.6,-80.55
 0.137071
ca,baden,Baden,08,43.4,-80.6666667
 0.161756
ca,floradale,Floradale,08,43.6166667,-80.5833333
 0.163351
ca,preston,Preston,08,43.4,-80.35
 0.181762
ca,ayr,Ayr,08,43.2833333,-80.45
 0.195739
---
Linear search took 143212
ca,waterloo,Waterloo,08,43.4666667,-80.5333333
 0.0141501
ca,kitchener,Kitchener,08,43.45,-80.5
 0.025264
ca,bridgeport,Bridgeport,08,43.4833333,-80.4833333
 0.0396333
ca,elmira,Elmira,08,43.6,-80.55
 0.137071
ca,baden,Baden,08,43.4,-80.6666667
 0.161756
ca,floradale,Floradale,08,43.6166667,-80.5833333
 0.163351
ca,preston,Preston,08,43.4,-80.35
 0.181762
ca,ayr,Ayr,08,43.2833333,-80.45
 0.195739

Construction

I'm too lazy to implement a delete or insert function. It is most efficient to simply build the tree by repeatedly partitioning the data. We build the tree from the top down from an array of items. For each node, we first choose a point at random, and then partition the list into two sets: The left children contain the points farther away than the median, and the right contains the points that are closer than the median. Then we recursively repeat this until we have run out of points.

// A VP-Tree implementation, by Steve Hanov. (steve.hanov@gmail.com)
// Released to the Public Domain
// Based on "Data Structures and Algorithms for Nearest Neighbor Search" by Peter N. Yianilos
#include <stdlib.h>
#include <algorithm>
#include <vector>
#include <stdio.h>
#include <queue>
#include <limits>

template<typename T, double (*distance)( const T&, const T& )>
class VpTree
{
public:
    VpTree() : _root(0) {}

    ~VpTree() {
        delete _root;
    }

    void create( const std::vector& items ) {
        delete _root;
        _items = items;
        _root = buildFromPoints(0, items.size());
    }

    void search( const T& target, int k, std::vector* results, 
        std::vector<double>* distances) 
    {
        std::priority_queue<HeapItem> heap;

        _tau = std::numeric_limits::max();
        search( _root, target, k, heap );

        results->clear(); distances->clear();

        while( !heap.empty() ) {
            results->push_back( _items[heap.top().index] );
            distances->push_back( heap.top().dist );
            heap.pop();
        }

        std::reverse( results->begin(), results->end() );
        std::reverse( distances->begin(), distances->end() );
    }

private:
    std::vector<T> _items;
    double _tau;

    struct Node 
    {
        int index;
        double threshold;
        Node* left;
        Node* right;

        Node() :
            index(0), threshold(0.), left(0), right(0) {}

        ~Node() {
            delete left;
            delete right;
        }
    }* _root;

    struct HeapItem {
        HeapItem( int index, double dist) :
            index(index), dist(dist) {}
        int index;
        double dist;
        bool operator<( const HeapItem& o ) const {
            return dist < o.dist;   
        }
    };

    struct DistanceComparator
    {
        const T& item;
        DistanceComparator( const T& item ) : item(item) {}
        bool operator()(const T& a, const T& b) {
            return distance( item, a ) < distance( item, b );
        }
    };

    Node* buildFromPoints( int lower, int upper )
    {
        if ( upper == lower ) {
            return NULL;
        }

        Node* node = new Node();
        node->index = lower;

        if ( upper - lower > 1 ) {

            // choose an arbitrary point and move it to the start
            int i = (int)((double)rand() / RAND_MAX * (upper - lower - 1) ) + lower;
            std::swap( _items[lower], _items[i] );

            int median = ( upper + lower ) / 2;

            // partitian around the median distance
            std::nth_element( 
                _items.begin() + lower + 1, 
                _items.begin() + median,
                _items.begin() + upper,
                DistanceComparator( _items[lower] ));

            // what was the median?
            node->threshold = distance( _items[lower], _items[median] );

            node->index = lower;
            node->left = buildFromPoints( lower + 1, median );
            node->right = buildFromPoints( median, upper );
        }

        return node;
    }

    void search( Node* node, const T& target, int k,
                 std::priority_queue& heap )
    {
        if ( node == NULL ) return;

        double dist = distance( _items[node->index], target );
        //printf("dist=%g tau=%gn", dist, _tau );

        if ( dist < _tau ) {
            if ( heap.size() == k ) heap.pop();
            heap.push( HeapItem(node->index, dist) );
            if ( heap.size() == k ) _tau = heap.top().dist;
        }

        if ( node->left == NULL && node->right == NULL ) {
            return;
        }

        if ( dist < node->threshold ) {
            if ( dist - _tau <= node->threshold ) {
                search( node->left, target, k, heap );
            }

            if ( dist + _tau >= node->threshold ) {
                search( node->right, target, k, heap );
            }

        } else {
            if ( dist + _tau >= node->threshold ) {
                search( node->right, target, k, heap );
            }

            if ( dist - _tau <= node->threshold ) {
                search( node->left, target, k, heap );
            }
        }
    }
};